Convex Hull
See also Minimum Enclosing Circle
| Function Syntax | (LM:ConvexHull <lst>) |
| Current Version | 1.0 |
| Download | ConvexHull.lsp |
| View HTML Version | ConvexHull.html |
| Donate |
| Arguments | ||
|---|---|---|
| Symbol | Type | Description |
| lst | List | List of coplanar points |
| Returns | ||
| Type | Description | |
| List | List of points describing Convex Hull | |
Program Description
The Convex Hull of a set of points is the point set describing the minimum convex polygon enclosing all points in the set.
There have been numerous algorithms of varying complexity and effiency, devised to compute the Convex Hull of a set of points. The function given on this page implements the Graham Scan Algorithm, a brief explanation and demonstration of which may be found below.
The Graham Scan Algorithm
The Graham Scan is an efficient algorithm for computing the Convex Hull of a set of points, with time complexity O(n log n). It is named after American Mathematician Ronald Graham, who published the algorithm in 1972.
Here is a brief outline of the Graham Scan algorithm:
- First, find the point with the lowest y-coordinate. If the lowest y-coordinate exists in more than one point in the set, the point with the lowest x-coordinate out of the candidates is chosen. Call this point P.
- Next, the set of points is sorted in increasing order of the angle they and the point P make with the x-axis.
- For each point in the sorted set: if the point and the two previously considered points form a clockwise path, this indicates that the previous point is not part of the Convex Hull and this point is discarded from the set.
- Continue until the last three points form an counter-clockwise path, then move on to the next point in the sorted set.
- This process will eventually iterate over all points in the sorted set, resulting in the set containing only those points on the convex hull boundary.
Demonstration of the Graham Scan Algorithm

Example Program 1
The following example program will prompt the user for a selection of points, then proceed to construct an LWPolyline describing the Convex Hull of the selection.
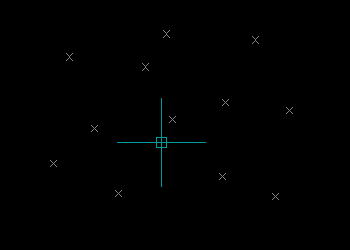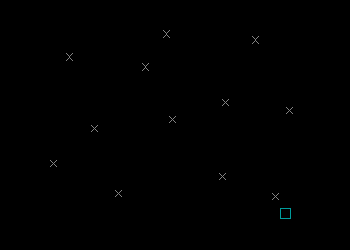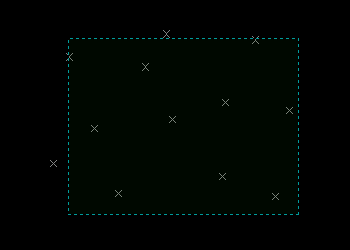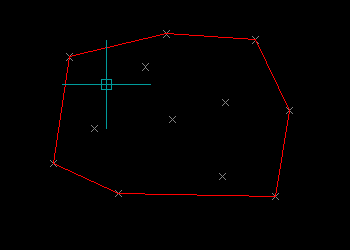
(defun c:test1 ( / i l s ) (if (setq s (ssget '((0 . "POINT")))) (progn (repeat (setq i (sslength s)) (setq l (cons (cdr (assoc 10 (entget (ssname s (setq i (1- i)))))) l)) ) (setq l (LM:ConvexHull l)) (entmakex (append (list '(000 . "LWPOLYLINE") '(100 . "AcDbEntity") '(100 . "AcDbPolyline") (cons 90 (length l)) '(070 . 1) ) (mapcar '(lambda ( x ) (cons 10 x)) l) ) ) ) ) (princ) )
Example Program 2
This alternative example will continuously prompt the user to pick a point and will construct the Convex Hull of the union of the selected point and all previous selected points.

(defun c:test2 ( / e l p ) (if (setq p (getpoint "\nPick 1st point: ")) (progn (setq p (trans p 1 0) l (list p) ) (entmake (list '(0 . "POINT") (cons 10 p))) (while (setq p (getpoint "\nPick next point <Exit>: ")) (setq p (trans p 1 0) l (LM:ConvexHull (cons p l)) ) (entmake (list '(0 . "POINT") (cons 10 p))) (if e (progn (entdel e) (setq e nil))) (setq e (entmakex (append (list '(000 . "LWPOLYLINE") '(100 . "AcDbEntity") '(100 . "AcDbPolyline") (cons 90 (length l)) '(070 . 1) ) (mapcar '(lambda ( x ) (cons 10 x)) l) ) ) ) ) ) ) (princ) )
See also Minimum Enclosing Circle
